二分搜索学习及扩展

二分搜索，很多人会有这样的想法：这不是是一个很简单的算法么？
刚开始学习编程的时候，就学到这个算法。

但是仔细研究一下发现，二分搜索并不是想像中那么简单的。Programming Pearls提到：

虽然第一篇二分搜索的论文是在1946年就发表了，但是第一个没有错误的二分搜的程序却在1962年才出现。

算法思想提出，到正确的实现居然跨越了16年，真心不简单啊。

这篇文章就是讨论二分搜索这个算法。

算法思想

二分搜索用到的思想——分治(conque and divide)。
每次搜索一次都把搜索范围减少一半，这样搜索的算法复杂度就为logn了。

下面来个经典的算法实现：

//find value in range:[l, r)
int binary_search(int l, int r, int value, int* array j)
{
    int m;
    while (l < r)
    {
        m = (l+r)/2;
        if (array[m] == value)
            return m;
        else if (array[m] < value)
            l = m+1;
        else
            r = m;
    }
    return -1;
}

上面的binary search的区间都是按照stl的区间表示法：左闭右开。

上面这个算法,很多算法书的实现。这就是标准的二分查迭代实现。

在绝大多数的情况下，这个算法都是正确的。在一个数组中搜索指定的元素value。

那就是代码中的求中间值这句： m = (l+r)/2;

l+r的计算结果有可能发生溢出。当l，r > MAX(int)/2时，l+r就会发生溢出，导致m计算的值为负数。
据说这个bug在java 1.2～1.5的Array.binarySearch一直存在，直到1.6才被修复。

这个情况非常少见，特别是在个人PC上一般而言,我们的程序没有那么大的数组，
试想一下，MAX(int)/2 = (2^32 - 1)/2, 我们就取2^30 好了，2^30 个int，得多大的内存？
2^30 4bytes = 2 32bytes = 4G。
在32位 linux下面，一个进程空间最大只能3G，因此，当开辟那么大的数组时，os也不允许。

但是如果采用二分搜索的思想求方程的根(例如求方程的零点)，那就不同了.
如果零点x > MAX(int)/2，那么问题就出现了。

避免溢出的正确做法应该改成这样：m = l+(r-l)/2;

要是把上面二分搜索的代码改成下面这种写法:

//find value in range:[l, r)
int binary_search(int l, int r, int value, int* array j)
{
    int m;
    while (l < r)
    {
        m = (l+r)/2;
        if (array[m] == value)
            return m;
        else if (array[m] < value)
            //l = m+1;
            l = m;
        else
            r = m;
    }
    return -1;
}

改动很简单，就是把l = m+1;
改成l = m;

看上去似乎没有问题，把条件放宽了，array[m] < value,说明value只能在[m,r)之间。

但可能会导致死循环，可以试试下面这个数数据：

n = 2
data[0] = 1, data[1] = 1;
value = 2;

算法最后会一直保持l=1，r=2。不会停止，因为m=(1+2)/2 = 1, l的值永远为1处。

扩展

如果数组中有多个重复的元素，二分搜索只会返回其任意一个位置。
那么就可以做下面的扩展了，
如果我想返回第一个出现的位置，怎么办？返回最后一个出现的位置，那又怎么办？

这就引申出lower_bound和upper_bound了。

lower_bound

C++ STL的algorithm已经提供了这个函数了，函数声明如下：

template <class ForwardIterator, class T>
ForwardIterator lower_bound ( ForwardIterator first, ForwardIterator last, const T& value )

函数作用如下：

• 如果搜索的value在数组中有多个重复，那么返回第一个。
• 如果搜索不到，则返回位置i，a[0] <= a[1] <= … <= a[i-1] < value < a[i] < …，文字表达就是把value插入位置i后，原数组顺序不变。

我们自己实现，该如何实现呢？只要把二分搜索的代码稍稍改动一点即可：

该如何实现呢？只要把二分搜索的代码稍稍改动一点即可：

int lower_bound(int l, int r, int value)
{
    int m;
    while (l < r)
    {
        int m = l + (r-l)/2;
        if (value == data[m])
            r = m;
        else if (value > data[m])
            l = m+1;
        else
            r = m;
    }
    return r;
}

思想很简单：

1. 当value == data[m]时，可以确定的位置i，在[l,m]中;
2. 当value > data[m]时,可以确定位置i在[m+1,r)区间中；
3. 当value < data[m]时,可以确定位置i在[l, m]中；

注意到第三种情况，区间是[l,m],包含m的，因为有可能在[l,m-1]区间中找不到元素=value。
因此m就是返回位置。

upper_bound

C++ STL中也同样提供了upper_bound的函数，声明如下：

template <class ForwardIterator, class T>
ForwardIterator upper_bound ( ForwardIterator first, ForwardIterator last, const T& value )

//如果搜索的value在数组中有多个重复，那么返回匹配元素最后一个位置的后一个位置。
//如果搜索不到，则返回位置i，a[0] <= a[1] <= ... <= a[i-1] < value < a[i] < ...，文字表达就是把value插入位置i后，原数组顺序不变。

值得注意的是，这个upper_bound函数不是想像中返回重复元素的最后一个位置，而是返回最后一个位置+1。

代码实现如下：

int upper_bound(int l, int r, int value, int* data)
{
    int m;

    while (l < r)
    {
        int m = l + (r-l)/2;
        if (value == data[m])
           l = m+1;
        else if (value < data[m])
           r = m;
        else
           l = m+1;
    }

    return l;
}

思路和lower_bound的类似，

1. 当value == data[m]时，返回的结果位于[m+1,r)中；右边可能还有。
2. 当value < data[m]时，返回结果位于[l, m]中； 左边可能还有。
3. 当value > data[m]时，返回结果位于[m+1,r)中；剔除左边的区间。

对于第2种情况的处理

r = m;

可能会难理解，不论是lower还是upper，候选区间是[l,r],并非[l,r),因为value的值有可能大于整个数组，这时返回的结果就是r了。

如果想要返回最后一个元素的位置，而不是后面一个，如何实现?

只要再添加一个变量，保存一下中间结果即可。

int upper_bound(int l, int r, int value)
{
    int m;

    int ans = -1;
    while (l < r)
    {
        int m = l + (r-l)/2;
        if (value == data[m])
        {
           ans = m;
           l = m+1;
        }
        else if (value < data[m])
           r = m;
        else
           l = m+1;
    }

    if (ans != -1)
        return ans;
    return l;
}

是否会死循环

上面的lower_bound和upper_bound实现，会不会发生死循环呢？

答案是不会的，我们以upper_bound为例，观察l和r的变化：

1. l每次变化都是m+1，l的值只会增大。
2. r每次变化都赋值为m，而m = floor((x+y)/2)的，因此r每次赋值只会越来越少。

综合上面两个情况，while循环的条件l<r，总会为false的。因此算法不会陷入死循环。

C++实现

cplusplus有关于lower_bound和upper_bound的说明和实现：

template <class ForwardIterator, class T>
ForwardIterator lower_bound ( ForwardIterator first, ForwardIterator last, const T& value )
{
  ForwardIterator it;
  iterator_traits<ForwardIterator>::difference_type count, step;
  count = distance(first,last);
  while (count>0)
  {
    it = first; step=count/2; advance (it,step);
    if (*it<value)                   // or: if (comp(*it,value)), for the comp version
      { first=++it; count-=step+1;  }
    else count=step;
  }
  return first;
}

template <class ForwardIterator, class T>
ForwardIterator upper_bound ( ForwardIterator first, ForwardIterator last, const T& value )
{
  ForwardIterator it;
  iterator_traits<ForwardIterator>::difference_type count, step;
  count = distance(first,last);
  while (count>0)
  {
    it = first; step=count/2; advance (it,step);
    if (!(value<*it))                 // or: if (!comp(value,*it)), for the comp version
      { first=++it; count-=step+1;  }
    else count=step;
  }
  return first;
}

上面的实现思路与前文说的基本相同。不同的是其实现是通过迭代实现的，并增加泛型的支持。
里面求中间值时，是通过count变量作为计数器实现的。不存在之前说的(l+r)/2的溢出问题。
这里的first相当与l，由于通过count计算中间的m，就没有r了。

Rotated Sorted Array

二分搜索除了用在有序的数组上外，还可以用在rotated sorted array上。

什么是rotated sorted array？下面这个就是rotated sorted array：

[3, 4, 5, 1, 2, 3]

就是把一个有序数组向左滚动，前面的元素补在后面。rotated sorted array向右滚动(rotate)数次后就变成一个有序数组。

二分搜索的思想同样可以在这种数组上查找一个数。

思路如下:

1. 容易知道，rotate array array是由两个有序的数组组成.并且这两个数组有大小关系的，一般是后面的有序数组比前面的有序数组都小，即a[n-1] < a[0];
   看下文两个图即可。

2. 每次二分搜索划分数组时，至少有1个子数组是有序的。
   因为要么中点m落在第一个有序范围，要么落在第二个有序范围。

3. 二分搜索每次迭代只需要找出有序的子数组，判断查找的value是否在里面即可。
   如何判断，只需判断出value的值是否在该数组的最左值和最右值之间即可（如假设划分后a[l…m]是有序的，只需判断a[l]<= value <= a[m]）即可。

下面两个图形象说明这点：

左边子数组有序：

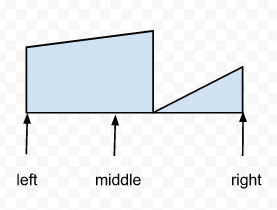
右边子数组有序：

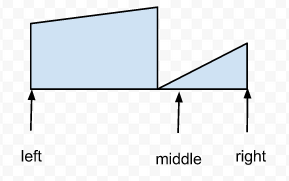
下面是代码:

//search range [l, r]
int binary_search(int l, int r, int value, int* data)
{
    while (l <= r)
    {
        int m = l + (r-l)/2;

        if (data[m] == value)
            return m;
        else if (data[m] < data[r]) //right part is sorted
        {
            if (value > data[m] && value <= data[r]) //check value whether in right part
                l = m+1;
            else
                r = m-1;
        }
        else //left part is sorted
        {
            if (value >= data[l] && value < data[m]) //check value whether in left part
               r = m-1;
            else
               l = m+1;
        }
    }
    return -1;
}

注意到上面的查找区间是[l, r]的。

总结

二分搜索真的不简单，在实现过程中稍有不慎，就会陷入错误。
在使用二分的思想写代码时，有下面两点需要注意：

1. 求中间值m时，注意溢出问题。
2. 仔细考虑左右区间的取值，稍有不慎，就会死循环了。这个可以使用2个相同的元素代进去，模拟一下，看算法是否会停止。

Update

2012.10.3 添加rotated sorted array部分。

Reference

1. Programming Pearls
2. upper_bound
3. lower_bound
4. WIKIPEDIA
5. searching-in-an-sorted-and-rotated-array